More
More
文章目录
  1. putVal
  2. putTreeVal
  3. find
  4. balanceInsertion
  5. rotateLeft/rotateRight
  6. treeifyBin
  7. 彩蛋
    1. untreeify/treeify

【java源码一带一路系列】之HashMap.putVal()

字数统计: 2.3k字   |   阅读时长: 12分钟
2017.05.14 Chen hongen 后端

回顾上期✈观光线路图：putAll() –> putMapEntries() –> tableSizeFor() –> resize() –> hash() –> putVal()…

本期与您继续一起砥砺前行：putVal() –> putTreeVal() –> find() –> balanceInsertion() –> rotateLeft()/rotateRight() –> treeifyBin()…

  • transient int modCount; 记录HashMap变更次数，用于的迭代时fail-fast；

putVal

新值的hash与key与map中已存在的值相等时，且原值不为null，根据onlyIfAbsent判断是否替换（true时不替换)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
               boolean evict) {
    Node<K,V>[] tab; Node<K,V> p; int n, i;
    if ((tab = table) == null || (n = tab.length) == 0)
        n = (tab = resize()).length;
    if ((p = tab[i = (n - 1) & hash]) == null)
        tab[i] = newNode(hash, key, value, null);
    else {
        Node<K,V> e; K k;
        if (p.hash == hash &&
            ((k = p.key) == key || (key != null && key.equals(k))))
            e = p;
        else if (p instanceof TreeNode)
            e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value); // ↓
        else {
	    // 遍历链表
            for (int binCount = 0; ; ++binCount) {
                if ((e = p.next) == null) {
                    p.next = newNode(hash, key, value, null);
                    if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st 因为binCount从0开始
                        treeifyBin(tab, hash); // ↓
                    break;
                }
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    break;
                p = e;
            }
        }
        if (e != null) { // existing mapping for key e不为null则表示已存在与map,值可能不同
            V oldValue = e.value;
            if (!onlyIfAbsent || oldValue == null)
                e.value = value;
            afterNodeAccess(e); /// 
            return oldValue;
        }
    }
    ++modCount;
    if (++size > threshold)
        resize();
    afterNodeInsertion(evict); /// 
    return null;
}

putTreeVal

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
// 为了找到合适的位置插入新节点，源码中进行了一系列比较。
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
                               int h, K k, V v) {
    Class<?> kc = null;
    boolean searched = false;
    TreeNode<K,V> root = (parent != null) ? root() : this; // 获取根节点，从根节点开始遍历
    for (TreeNode<K,V> p = root;;) {
        int dir, ph; K pk;
        if ((ph = p.hash) > h)
            dir = -1; // 左
        else if (ph < h)
            dir = 1; // 右
        else if ((pk = p.key) == k || (k != null && k.equals(pk)))
            return p; // 此时hash,key相等,直接返回
        else if ((kc == null &&
                  (kc = comparableClassFor(k)) == null) ||
                 (dir = compareComparables(kc, k, pk)) == 0) {
            if (!searched) {
                TreeNode<K,V> q, ch;
                searched = true;
                if (((ch = p.left) != null &&
                     (q = ch.find(h, k, kc)) != null) ||
                    ((ch = p.right) != null &&
                     (q = ch.find(h, k, kc)) != null))
                    return q; // 左右子树存在，则返回
            }
            dir = tieBreakOrder(k, pk);
        }
        TreeNode<K,V> xp = p;
        if ((p = (dir <= 0) ? p.left : p.right) == null) {
            Node<K,V> xpn = xp.next;
            TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);
            if (dir <= 0) // 即p.left == null
                xp.left = x;
            else
                xp.right = x;
            xp.next = x;
            x.parent = x.prev = xp;
            if (xpn != null)
                ((TreeNode<K,V>)xpn).prev = x;
            moveRootToFront(tab, balanceInsertion(root, x));
            return null;
        }
    }
}

当前节点hash值(ph)与插入节点hash值(h)比较，
若ph > h(dir=-1)，将新节点归为左子树;
若ph < h(dir=1)，右子树;
否则即表示hash值相等，然后又对key进行了比较。

“kc = comparableClassFor(k)) == null”表示该类本身不可比（class C don’t implements Comparable）；“dir = compareComparables(kc, k, pk)) == 0”表示k与pk对应的Class之间不可比。searched为一次性开关仅在p为root时生效，遍历比较左右子树中是否存在于插入节点相等的。

最后比到tieBreakOrder()中的“System.identityHashCode(a) <= System.identityHashCode(b)”，即对象的内存地址来生成的hashCode相互比较。堪称铁杵磨成针的比较。

这里循环的推进是靠“if ((p = (dir <= 0) ? p.left : p.right) == null)”，之前千辛万苦比较出的dir也在这使用。直到为空的左/右子树节点，插入新值（新值插入的过程参考下图理解）。
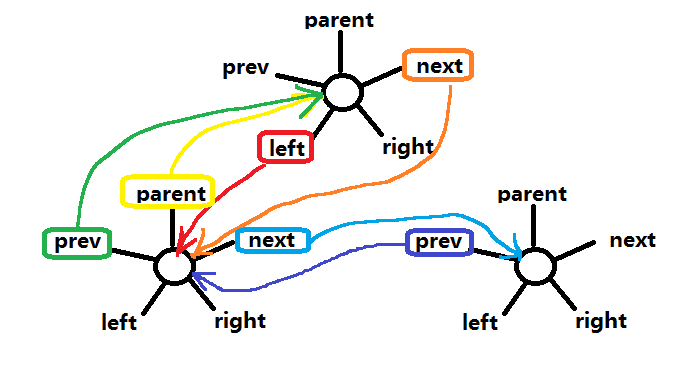
image

find

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
final TreeNode<K,V> find(int h, Object k, Class<?> kc) {
    TreeNode<K,V> p = this;
    do {
        int ph, dir; K pk;
        TreeNode<K,V> pl = p.left, pr = p.right, q;
        if ((ph = p.hash) > h)
            p = pl;
        else if (ph < h)
            p = pr;
        else if ((pk = p.key) == k || (k != null && k.equals(pk)))
            return p;
        else if (pl == null)
            p = pr;
        else if (pr == null)
            p = pl;
        else if ((kc != null ||
                  (kc = comparableClassFor(k)) != null) &&
                 (dir = compareComparables(kc, k, pk)) != 0)
            p = (dir < 0) ? pl : pr;
        else if ((q = pr.find(h, k, kc)) != null)
            return q;
        else
            p = pl;
    } while (p != null);
    return null;
}

有没有发现，如果当你看懂putTreeVal，类比find是不是变得很好理解了呢？

balanceInsertion

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
                                                    TreeNode<K,V> x) {
    x.red = true; // x为红
    for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
        // x为根
        if ((xp = x.parent) == null) {
            x.red = false;
            return x;
        }
        // x父节点为黑 || x父节点为根（黑）
        else if (!xp.red || (xpp = xp.parent) == null)
            return root;
        // 
        if (xp == (xppl = xpp.left)) {
            // ①
            if ((xppr = xpp.right) != null && xppr.red) {
                xppr.red = false;
                xp.red = false;
                xpp.red = true;
                x = xpp;
            }
            // ②
            else {
                if (x == xp.right) {
                    root = rotateLeft(root, x = xp);
                    xpp = (xp = x.parent) == null ? null : xp.parent;
                }
                if (xp != null) {
                    xp.red = false;
                    if (xpp != null) {
                        xpp.red = true;
                        root = rotateRight(root, xpp);
                    }
                }
            }
        }
        else {
            if (xppl != null && xppl.red) {
                xppl.red = false;
                xp.red = false;
                xpp.red = true;
                x = xpp;
            }
            else {
                if (x == xp.left) {
                    root = rotateRight(root, x = xp);
                    xpp = (xp = x.parent) == null ? null : xp.parent;
                }
                if (xp != null) {
                    xp.red = false;
                    if (xpp != null) {
                        xpp.red = true;
                        root = rotateLeft(root, xpp);
                    }
                }
            }
        }
    }
}

在插入新值后，可能打破了红黑树原有的“平衡”，balanceInsertion()的作用就是要维持这种“平衡”，保证最佳效率。所谓的红黑树“平衡”即：

①：所有节点非黑即红；

②：根为黑，叶子为null且为黑，红的两子节点为黑；

③：任一节点到叶子节点的黑子节点个数相同；

下面，以“(xp == (xppl = xpp.left))”简(chou)单(lou)的给大家画个图例（其中①②与源码注释相对应）。
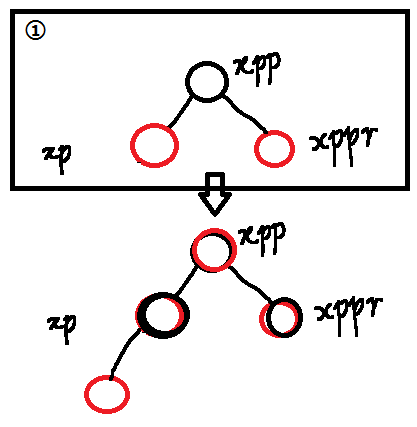
image

图②中打钩的都是合格的红黑树其实，图②右边方框内为左旋右旋节点关系变化图解。
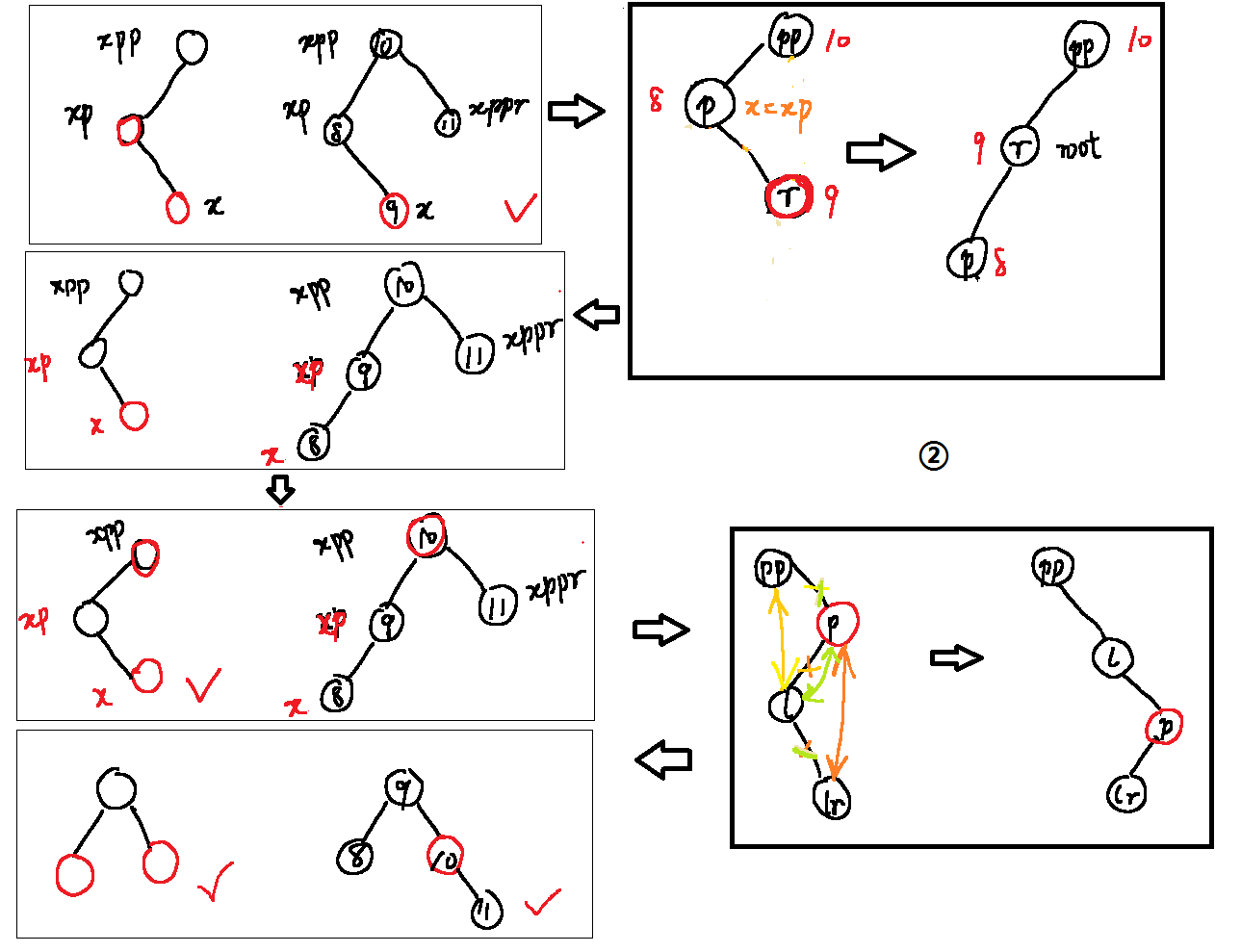
image

rotateLeft/rotateRight

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// 左旋 与 右旋
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root, TreeNode<K,V> p) {
    TreeNode<K,V> r, pp, rl;
    if (p != null && (r = p.right) != null) {
        if ((rl = p.right = r.left) != null)
            rl.parent = p;
        if ((pp = r.parent = p.parent) == null)
            (root = r).red = false;
        else if (pp.left == p)
            pp.left = r; // p为pp左子节点
        else
            pp.right = r;
        r.left = p;
        p.parent = r;
    }
    return root;
}
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root, TreeNode<K,V> p) {
    TreeNode<K,V> l, pp, lr;
    if (p != null && (l = p.left) != null) {
        if ((lr = p.left = l.right) != null)
            lr.parent = p;
        if ((pp = l.parent = p.parent) == null)
            (root = l).red = false;
        else if (pp.right == p)
            pp.right = l;
        else
            pp.left = l;
        l.right = p;
        p.parent = l;
    }
    return root;
}

左旋右旋过程包含在上面的图例中了，另附上两张网上看到的动图便于大家理解。

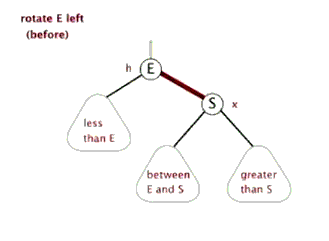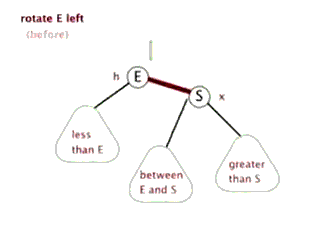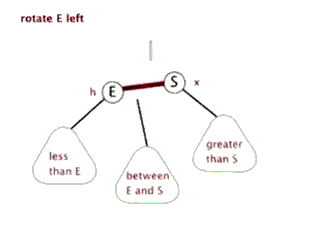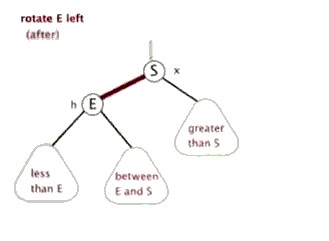
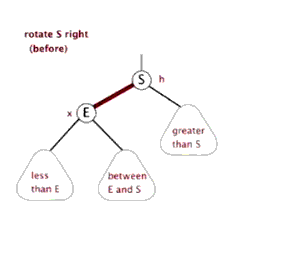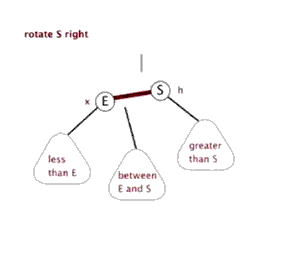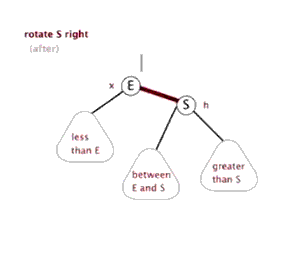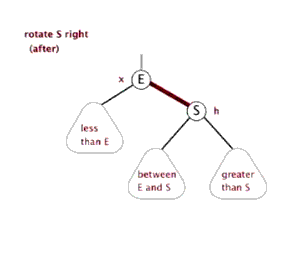
image

image

同时，在线红黑树插入删除动画演示【点我】，还不理解的童鞋可以亲自直观的试试。

treeifyBin

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
final void treeifyBin(Node<K,V>[] tab, int hash) {
    int n, index; Node<K,V> e;
    if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
        resize();
    else if ((e = tab[index = (n - 1) & hash]) != null) {
        TreeNode<K,V> hd = null, tl = null;
        do {
            TreeNode<K,V> p = replacementTreeNode(e, null);
            if (tl == null)
                hd = p;
            else {
                p.prev = tl;
                tl.next = p;
            }
            tl = p;
        } while ((e = e.next) != null);
        if ((tab[index] = hd) != null)
            hd.treeify(tab);
    }
}

putVal()的treeifyBin()在链表中数目大于等于“TREEIFY_THRESHOLD - 1”时触发。当数目满足MIN_TREEIFY_CAPACITY时，链表将转为红黑树结构，否则继续扩容。treeify()类似putTreeVal()。

彩蛋

在上一篇中的resize方法中，当节点类型为树时，有个TreeNode.split方法这里稍作补充/温习。整体思路与上篇提到的链表相似，根据hash&bit(即oldCap)的结果拆分成保留顺序的高低两部分。只是变成了构造树（统一归于本篇来讲树）。值得注意的是，当拆完的树长度小于一定值便“降级”为链表。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) {
    TreeNode<K,V> b = this;
    // Relink into lo and hi lists, preserving order
    TreeNode<K,V> loHead = null, loTail = null;
    TreeNode<K,V> hiHead = null, hiTail = null;
    int lc = 0, hc = 0;
    for (TreeNode<K,V> e = b, next; e != null; e = next) {
	next = (TreeNode<K,V>)e.next;
	e.next = null;
	if ((e.hash & bit) == 0) {
	    if ((e.prev = loTail) == null)
		loHead = e;
	    else
		loTail.next = e;
	    loTail = e;
	    ++lc;
	}
	else {
	    if ((e.prev = hiTail) == null)
		hiHead = e;
	    else
		hiTail.next = e;
	    hiTail = e;
	    ++hc;
	}
    }
    if (loHead != null) {
	if (lc <= UNTREEIFY_THRESHOLD)
	    tab[index] = loHead.untreeify(map);
	else {
	    tab[index] = loHead;
	    if (hiHead != null) // (else is already treeified)
		loHead.treeify(tab);
	}
    }
    if (hiHead != null) {
	if (hc <= UNTREEIFY_THRESHOLD)
	    tab[index + bit] = hiHead.untreeify(map);
	else {
	    tab[index + bit] = hiHead;
	    if (loHead != null)
		hiHead.treeify(tab);
	}
    }
}

untreeify/treeify

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
final Node<K,V> untreeify(HashMap<K,V> map) {
    Node<K,V> hd = null, tl = null;
    for (Node<K,V> q = this; q != null; q = q.next) {
	Node<K,V> p = map.replacementNode(q, null);
	if (tl == null)
	    hd = p;
	else
	    tl.next = p;
	tl = p;
    }
    return hd;
}
final void treeify(Node<K,V>[] tab) {
    TreeNode<K,V> root = null;
    for (TreeNode<K,V> x = this, next; x != null; x = next) {
	next = (TreeNode<K,V>)x.next;
	x.left = x.right = null;
	if (root == null) {
	    x.parent = null;
	    x.red = false;
	    root = x;
	}
	else {
	    K k = x.key;
	    int h = x.hash;
	    Class<?> kc = null;
	    for (TreeNode<K,V> p = root;;) {
		int dir, ph;
		K pk = p.key;
		if ((ph = p.hash) > h)
		    dir = -1;
		else if (ph < h)
		    dir = 1;
		else if ((kc == null &&
			  (kc = comparableClassFor(k)) == null) ||
			 (dir = compareComparables(kc, k, pk)) == 0)
		    dir = tieBreakOrder(k, pk);
		TreeNode<K,V> xp = p;
		if ((p = (dir <= 0) ? p.left : p.right) == null) {
		    x.parent = xp;
		    if (dir <= 0)
			xp.left = x;
		    else
			xp.right = x;
		    root = balanceInsertion(root, x);
		    break;
		}
	    }
	}
    }
    moveRootToFront(tab, root);
}
打赏
手机扫一扫，支持CHE~